This Math Problem for 10-Year-Olds Is Stumping the Internet. Can You Solve It?
Years ago, when a kid stumbled over a problem so tough they couldn't finish their math homework, they'd accept a less-than-perfect grade. Now, you can just ask the internet for help.
Read more: Can You Solve This Math Problem That's Stumping the Whole Internet? (Part 1)
Another seemingly simple math problem is going viral and stumping the Internet. It comes from a 10-year-old Year 5 student in Glossop, England. Confused, the kid asked his grandmother for advice. She couldn't figure it out, so the kid's dad took to Facebook to crowdsource an answer, and it went viral. Then, the Manchester Evening News picked up the story and asked its Twitter followers for help.
Eventually, readers figured out an answer. But before we give it away, see if you can solve it. The problem is easier than you think — it's basic geometry — but there's one confusing element that might screw you up.
We'll walk you through it with the help of Matthew Zaremsky, a math professor at Binghamton University. He advised Mic on the last problem, too.
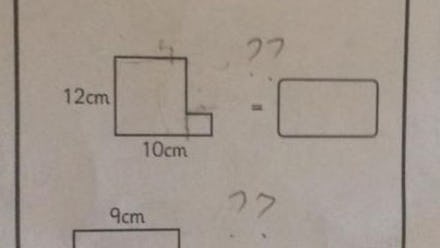
The first one is pretty simple.
To figure it out, start with the top side, (a). We know immediately that (e) is 10cm and (f) is 12cm. "But we also know that (a)+(c) is 10cm and (b)+(d) is 12cm," Zaremsky explains. "Hence the total perimeter a+b+c+d+e+f is (a+c)+(b+d)+e+f = 10+12+10+12 = 44."
The second problem is tougher — but it's not your fault.
According to Zaremsky, "If we again start at the top left corner and go clockwise to name the edges (a) through (h), then we get a+b+c+d+e+f+g+h = a+b+(c+e+g)+(d+h-f)+2f = 9+11+9+11+4=44."
That "2cm" label screwed up a lot of people. Which side is it labeling? It looks like it's side (e), but it's not — it's (f).
The 2cm "has to be labeling the side to its left for the problem to be doable," Zaremsky said. "If it's labeling (e), there's no way to uniquely solve this."
Why is it so tough? According to Zaremsky, "I think that ambiguous label is the only thing making this a 'bad' problem — but yeah, it's definitely pretty hard for a 10-year-old."